TLS computational DoS mitigation

Vincent Bernat November 1, 2011

Some days ago, a hacker group, THC, released a denial of service tool for TLS web servers. As stated in its description, the problem is not really new: a complete TLS handshake implies costly cryptographic computations.

There are two different aspects in the presented attack:

The computation cost of a handshake is more important for the server than for the client. The advisory explains that a server will require 15 times the processing power of a client. This means a single average workstation could challenge a multi-core high-end server.
TLS renegotiation allows you to trigger hundreds of handshakes in the same TCP connection. Even a client behind a DSL connection can therefore bomb a server with a lot of renegotiation requests.

Update (2015-02)

While the content of this article is still technically sound, ensure you understand it was written by the end of 2011 and therefore doesn’t take into account many important aspects, like the fall of RC4 as an appropriate cipher.

Mitigation techniques
Things get worse

Mitigation techniques#

There is no definitive solution to this attack but there exists some workarounds. Since the DoS tool from THC relies heavily on renegotiation, the most obvious one is to disable this mechanism on the server side but we will explore other possibilities.

Disabling TLS renegotiation#

Tackling the second problem seems easy: just disable TLS renegotiation. It is hardly needed: a server can trigger a renegotiation to ask a client to present a certificate but a client usually does not have any reason to trigger one. Because of a past vulnerability in TLS renegotiation, recent versions of Apache and nginx just forbid it, even when the non-vulnerable version is available.

openssl s_client can be used to test if TLS renegotiation is really disabled. Sending R on an empty line triggers renegotiation. Here is an example where renegotiation is disabled (despite being advertised as supported):

$ openssl s_client -connect www.luffy.cx:443 -tls1
[…]
New, TLSv1/SSLv3, Cipher is DHE-RSA-AES256-SHA
Server public key is 2048 bit
Secure Renegotiation IS supported
Compression: zlib compression
Expansion: zlib compression
[…]
R
RENEGOTIATING
140675659794088:error:1409E0E5:SSL routines:SSL3_WRITE_BYTES:ssl handshake failure:s3_pkt.c:591:

Disabling renegotiation is not trivial with OpenSSL. As an example, I have pushed a patch to disable renegotiation in stud, the scalable TLS unwrapping daemon.

Rate limiting TLS handshakes#

Disabling TLS renegotiation on the client side is not always possible. For example, your web server may be too old to propose such an option. Since these renegotiations should not happen often, a workaround is to limit them.

When the flaw was first advertised, F5 Networks provided a way to configure such a limitation with an iRule on their load-balancers. We can do something similar with Netfilter. We can spot most TCP packets triggering such a renegotiation by looking for encrypted TLS handshake record. They may happen in a regular handshake but in this case, they usually are not at the beginning of the TCP payload. There is no field saying if a TLS record is encrypted or not (TLS is stateful for this purpose). Therefore, we have to use some heuristics. If the handshake type is unknown, we assume that this is an encrypted record. Moreover, renegotiation requests are usually encapsulated in a TCP packet flagged with “push.”

# Access to TCP payload (if not fragmented)
payload="0 >> 22 & 0x3C @ 12 >> 26 & 0x3C @"
iptables -A LIMIT_RENEGOTIATION \
    -p tcp --dport 443 \
    --tcp-flags SYN,FIN,RST,PSH PSH \
    -m u32 \
    --u32 "$payload 0 >> 8 = 0x160300:0x160303 && $payload 2 & 0xFF = 3:10,17:19,21:255" \
    -m hashlimit \
    --hashlimit-above 5/minute --hashlimit-burst 3 \
    --hashlimit-mode srcip --hashlimit-name ssl-reneg \
    -j DROP

The use of u32 match is a bit difficult to read. The manual page gives some insightful examples. $payload allows us to seek for the TCP payload. It only works if there is no fragmentation. Then, we check if we have a handshake (0x16) and if we recognise TLS version (0x0300, 0x0301, 0x0302 or 0x0303). At last, we check if the handshake type is not a known value.

There is a risk of false positives but since we use hashlimit, we should be safe. This is not a bulletproof solution: TCP fragmentation would allow an attacker to evade detection. Another equivalent solution would be to use CONNMARK to record the fact the initial handshake has been done and forbid any subsequent handshakes.¹

If you happen to disable TLS renegotiation, you can still use some Netfilter rule to limit the number of TLS handshakes by limiting the number of TCP connections from one IP:

iptables -A LIMIT_TLS \
    -p tcp --dport 443 \
    --syn -m state --state NEW \
    -m hashlimit \
    --hashlimit-above 120/minute --hashlimit-burst 20 \
    --hashlimit-mode srcip --hashlimit-name ssl-conn \
    -j DROP

Your servers will still be vulnerable to a large botnet but if there is only a handful of source IP, this rule will work just fine.²

I have made all these solutions available in a single file.

Increasing server-side processing power#

TLS can easily be scaled up and out. Since TLS performance increases linearly with the number of cores, scaling up can be done by throwing in more CPU or more cores per CPU. Adding expensive TLS accelerators would also do the trick. Scaling out is also relatively easy but you should care about TLS session resume.

Putting more work on the client#

In their presentation of the denial of service tool, THC explains:

Establishing a secure SSL connection requires 15× more processing power on the server than on the client.

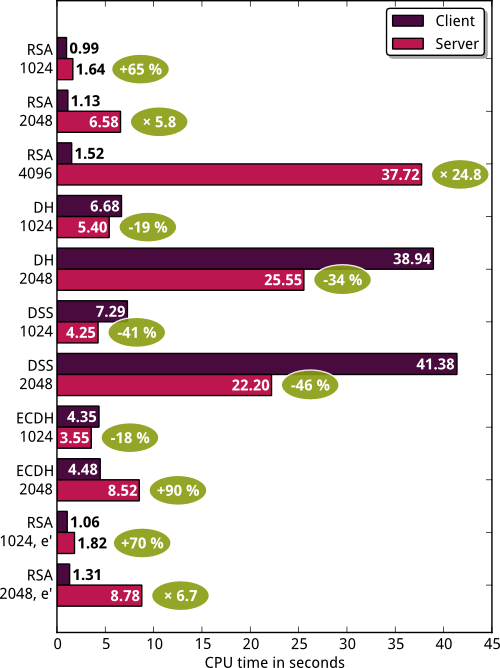
I don’t know where this figure comes from. To check it, I built a small tool to measure CPU time of a client and a server doing 1000 handshakes with various parameters (cipher suites and key sizes). The results are summarized on the following plot:

Plot to compare computational power required by servers and clients — Comparison of computational power needed by servers and clients

Update (2011-11)

Adam Langley announced Google HTTPS sites now support forward secrecy and ECDHE-RSA-RC4-SHA is now the preferred cipher suite thanks to fast, constant-time implementations of elliptic curves P-224, P-256 and P-521 in OpenSSL. The tests above did not use these implementations.

For example, with 2048-bit RSA certificates and a cipher suite like AES256-SHA, the server needs 6 times more CPU power than the client. However, if we use DHE-RSA-AES256-SHA instead, the server needs 34% less CPU power. The most efficient cipher suite from the server point of view seems to be something like DHE-DSS-AES256-SHA where the server needs half the power of the client.

However, you can’t really use only these shiny cipher suites:

Some browsers do not support them: they are limited to RSA cipher suites.³
Using them will increase your regular load a lot. Your servers may collapse with just legitimate traffic.
They are expensive for some mobile clients: they need more memory, more processing power and will drain battery faster.

Let’s dig a bit more into why the server needs more computational power in the case of RSA. Here is a TLS handshake when using a cipher suite like AES256-SHA:

When sending the Client Key Exchange message, the client will encrypt TLS version and 46 random bytes with the public key of the certificate sent by the server in its Certificate message. The server will have to decrypt this message with its private key. These are the two most expensive operations in the handshake. Encryption and decryption are done with RSA (because of the selected cipher suite). To understand why decryption is more expensive than encryption, let me explain how RSA works.

First, the server needs a public and a private key. Here are the main steps to generate them:

Pick two random distinct prime numbers $p$ and $q$ , each roughly the same size.
Compute $n=pq$ . It is the modulus.
Compute $\varphi(n)=(p-1)(q-1)$ .
Choose an integer $e$ such that $1<e<\varphi(n)$ and $\gcd(\varphi(n),e) = 1$ (i.e. $e$ and $\varphi(n)$ are coprime). It is the public exponent.
Compute $d=e^{-1}\bmod\varphi(n)$ . It is the private key exponent.

The public key is $(n,e)$ while the private key is $(n,d)$ . A message to be encrypted is first turned into an integer $m<n$ (with some appropriate padding). It is then encrypted to a ciphered message $c$ with the public key and should only be decrypted with the private key:

$c=m^e\bmod n$ (encryption)
$m=c^d\bmod n$ (decryption)

So, why is decryption more expensive? In fact, the key pair is not really generated as I described above. Usually, $e$ is a small fixed prime number with a lot of 0, like 17 (0x11) or 65537 (0x10001) and $p$ and $q$ are chosen such that $\varphi(n)$ is coprime with $e$ . This allows encryption to be fast using exponentiation by squaring. On the other hand, its inverse $d$ is a big number with no special property and therefore, exponentiation is more costly and slow.

Instead of computing $d$ from $e$ , it is possible to choose $d$ and compute $e$ . We could choose $d$ to be small and coprime with $\varphi(n)$ and then compute $e=d^{-1}\bmod\varphi(n)$ and get blazingly fast decryption. Unfortunately, there are two problems with this:

Most TLS implementations expect $e$ to be a 32-bit integer.
If $d$ is too small (less than one-quarter as many bits as the modulus $n$ ), it can be computed efficiently from the public key.

Therefore, we cannot use a small private exponent. The best we can do is to choose the public exponent to be $e'=4294967291$ (the biggest prime 32-bit number and it contains only one 0). However, there is no change as you can see on our comparative plot.

To summarize, no real solution here. You need to allow RSA cipher suites and there is no way to improve the computational ratio between the server and the client with such a cipher suite.

Things get worse#

Shortly after the release of the denial of service tool, Eric Rescorla⁴ published a good analysis on the impact of such a tool. He asks himself about the efficiency to use renegotiation for such an attack:

What you should be asking at this point is whether a computational DoS attack based on renegotiation is any better for the attacker than a computational DoS attack based on multiple connections. The way we measure this is by the ratio of the work the attacker has to do to the work that the server has to do. I’ve never seen any actual measurements here (and the THC guys don’t present any), but some back of the envelope calculations suggest that the difference is small.

If I want to mount the old, multiple connection attack, I need to incur the following costs:

Do the TCP handshake (3 packets)

Send the SSL/TLS ClientHello (1 packet). This can be a canned message.

Send the SSL/TLS ClientKeyExchange, ChangeCipherSpec, Finished messages (1 packet). These can also be canned.

Note that I don’t need to parse any SSL/TLS messages from the server, and I don’t need to do any cryptography. I’m just going to send the server junk anyway, so I can (for instance) send the same bogus ClientKeyExchange and Finished every time. The server can’t find out that they are bogus until it’s done the expensive part. So, roughly speaking, this attack consists of sending a bunch of canned packets in order to force the server to do one RSA decryption.

I have written a quick proof of concept of such a tool. To avoid any abuse, it will only work if the server supports NULL-MD5 cipher suite. No sane server in the wild will support such a cipher. You need to configure your web server to support it before using this tool.

While Eric explains that there is no need to parse any TLS messages, I have found that if the key exchange message is sent before the server sends the answer, the connection will be aborted. Therefore, I quickly parse the server’s answer to check if I can continue. Eric also says a bogus key exchange message can be sent since the server will have to decrypt it before discovering it is bogus. I have chosen to build a valid key exchange message during the first handshake (using the certificate presented by the server) and replay it on subsequent handshakes because I think the server may dismiss the message before the computation is complete (for example, if the size does not match the size of the certificate).

Update (2011-11)

Michał Trojnara has written sslsqueeze, a similar tool. It uses libevent2 library and should display better performance than mine. It does not compute a valid key exchange message but ensures the length is correct.

With such a tool and 2048-bit RSA certificate, a server is using 100 times more processing power than the client. Unfortunately, this means that most solutions, except rate limiting, exposed on this page may just be ineffective.