TLS & Perfect Forward Secrecy
Vincent Bernat
Once the private key of some HTTPS web site is compromised, an attacker is able to build a man-in-the-middle attack to intercept and decrypt any communication with the web site. The first step against such an attack is the revocation of the associated certificate through a CRL or a protocol like OCSP. Unfortunately, the attacker could also have recorded past communications protected by this private key and therefore decrypt them.
Forward secrecy allows today information to be kept secret even if the private key is compromised in the future. Achieving this property is usually costly and therefore, most web servers do not enable it on purpose. Google recently announced support of forward secrecy on their HTTPS sites. Adam Langley wrote a post with more details on what was achieved to increase efficiency of such a mechanism: with a few fellow people, he wrote an efficient implementation of some elliptic curve cryptography for OpenSSL.
Update (2019-08)
While the content of this article is still technically sound, ensure you understand it was written by the end of 2011 and therefore doesn’t take into account many important aspects, like the fall of RC4 as an appropriate cipher and the ubiquity of forward secrecy in actual deployments.
Without forward secrecy#
To understand the problem when forward secrecy is absent, let’s look
at the classic TLS handshake when using a cipher suite like
AES128-SHA. During this handshake, the server will present its
certificate and both the client and the server will agree on a master
secret.

This secret is built from a 48byte premaster secret generated and encrypted by the client with the public key of the server. It is then sent in a Client Key Exchange message to the server during the third step of the TLS handshake. The master secret is derived from this premaster secret and random values sent in clear-text with Client Hello and Server Hello messages.
This scheme is secure as long as only the server is able to decrypt the premaster secret (with its private key) sent by the client. Let’s suppose that an attacker records all exchanges between the server and clients during a year. Two years later, the server is decommissioned and sent for recycling. The attacker is able to recover the hard drive with the private key. They can now decrypt any session they recorded: the encrypted premaster secret sent by a client is decrypted with the private key and the master secret is derived from it. The attacker can now recover passwords and other sensitive information that can still be valuable today.
The main problem lies in the fact that the private key is used for two purposes: authentication of the server and encryption of a shared secret. Authentication only matters while the communication is established, but encryption is expected to last for years.
Diffie-Hellman with discrete logarithm#
One way to solve the problem is to keep using the private key for authentication but uses an independent mechanism to agree on a shared secret. Hopefully, there exists a well-known protocol for this: the Diffie-Hellman key exchange. It is a method of exchanging keys without any prior knowledge. Here is how it works in TLS:
-
The server needs to generate once (for example, with
openssl dhparamcommand):, a large prime number, , a primitive root modulo —for every integer coprime to , there exists an integer such that .
-
The server picks a random integer
and compute . After sending its regular Certificate message, it will also send a Server Key Exchange message (not included in the handshake depicted above) containing, unencrypted but signed with its private key for authentication purpose: - random value from the Client Hello message,
- random value from the Server Hello message,
, , .
-
The client checks that the signature is correct. It also picks a random integer
and sends in a Client Key Exchange message. It will also compute which is the premaster secret from which the master secret is derived. -
The server will receive
and compute which is the same premaster secret known by the client.
Again, the private key is only used for authentication purpose. An
eavesdropper will only know
Because the Diffie-Hellman exchange described above always uses new
random values DHE-RSA-AES128-SHA use this
protocol to achieve perfect forward secrecy.1
To achieve a good level of security, parameters of the same size as the key are usually used (the security provided by the discrete logarithm problem is about the same as the security provided by factorisation of two large prime numbers) and therefore, the exponentiation operations are pretty slow as we can see in the benchmark below:
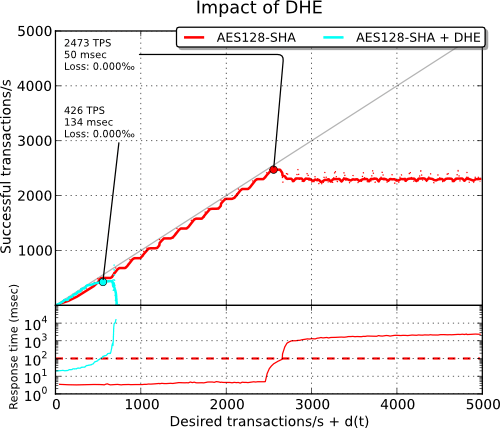
Update (2015-05)
The Logjam attack demonstrated that the security of Diffie-Hellman is lower than expected, notably when the prime is shared by many servers as this is usually the case. In this case, an attack against this prime can be precomputed and used to efficiently break connections using the same prime. Ensure that the DH parameter matches the size of the associated RSA key (at least 2048 bits).
Diffie-Hellman with elliptic curves#
Fortunately, there exists another way to achieve a Diffie-Hellman key exchange with the help of elliptic curve cryptography which is based on the algebraic structure of elliptic curves over finite fields. To get some background on this, be sure to check first Wikipedia article on elliptic curves. Elliptic curve cryptography allows one to achieve the same level of security than RSA with smaller keys. For example, a 224-bit elliptic curve is believed to be as secure as a 2048-bit RSA key.
Some theory#
Diffie-Hellman key exchange described above can easily be translated
to elliptic curves. Instead of defining
The use of elliptic curves is an extension of TLS described in RFC 4492. Unlike with the classic Diffie-Hellman key exchange, the client and the server need to agree on the various parameters. Most of this agreement is done inside Client Hello and Server Hello messages. While it is possible to define some arbitrary parameters, web browsers will only support a handful of predefined curves, usually NIST P-256, P-384 and P-521. From here, the key exchange with elliptic curves is pretty similar to the classic Diffie-Hellman one:
- The server picks a random integer
and compute which will be sent, unencrypted but signed with its private key for authentication purpose, in a Server Key Exchange message. - The client checks that the signature is correct. It also picks a
random integer
and sends in a Client Key Exchange message. It will also compute which is the premaster secret from which the master secret is derived. - The server will receive
and compute which is the same premaster secret known by the client.
An eavesdropper will only see
Using ECDHE-RSA-AES128-SHA cipher suite (with P-256 for example) is
already a huge speed improvement over DHE-RSA-AES128-SHA thanks to
the reduced size of the various parameters involved.
Web browsers only support a handful of well-defined elliptic curves, chosen to ease an efficient implementation. Bodo Möller, Emilia Käsper and Adam Langley have provided 64-bit optimized versions of NIST P-224, P-256 and P-521 for OpenSSL. To get even more details on the matter, you can read the end of the introduction on elliptic curves from Adam Langley, then a short paper from Emilia Käsper which presents a 64-bit optimized implementation of the NIST elliptic curve NIST P-224.
In practice#
First, keep in mind that elliptic curve cryptography is not supported by all browsers. Recent versions of Firefox and Chrome should handle NIST P-256, P-384 and P-521 but for Internet Explorer on Windows XP, you are currently out of luck. Therefore, you need to keep accepting other cipher suites.
You need a recent version of OpenSSL. Support for ECDHE cipher suites
has been added in OpenSSL 1.0.0. Check with openssl ciphers ECDH
that your version supports them. If you want to use the 64-bit
optimized version, you need to run a snapshot of OpenSSL 1.0.1,
configured with enable-ec_nistp_64_gcc_128 option. A recent GCC is
also required in this case.
Next, you need to choose the appropriate cipher suites. If
forward secrecy is an option for you, you can opt for
ECDHE-RSA-AES128-SHA:AES128-SHA:RC4-SHA cipher suites which should be
compatible with most browsers. If you really need forward secrecy, you
may opt for
ECDHE-RSA-AES128-SHA:DHE-RSA-AES128-SHA:EDH-DSS-DES-CBC3-SHA
instead.
Then, you need to ensure the order of cipher suites is
respected. On nginx, this is done with ssl_prefer_server_ciphers
on. On Apache, this is SSLHonorCipherOrder on.
Update (2011-11)
You need to check ECDHE support for your web
server. For nginx, the support has been added in 1.0.6 and
1.1.0. The curve selected defaults to NIST P-256. You can specify
another one with ssl_ecdh_curve directive. For Apache, it has been
added in 2.3.3 and does not exist in the current stable branch. Adding
support for ECDHE is quite easy. You can check how I added it in
stud. This issue also exists for DHE cipher suites, in
which case you also might have to specify DH parameters to use
(generated with openssl dhparam) using some special directive or by
appending the parameters to the certificate. Check Immerda Techblog
article for more background about this point.
The implementation of TLS session tickets may be incompatible with forward secrecy, depending on how they are implemented. When they are protected by a random key generated at the start of the server, the same key could be used for months. Some implementations2 may derive the key from the private key. In this case, forward secrecy is broken. If forward secrecy is a requirement for you, you need to either disable tickets or ensure that key rotation happens often.
Check with openssl s_client -tls1 -cipher ECDH -connect
127.0.0.1:443 that everything works as expected.
Some benchmarks#
With the help of the micro-benchmark tool that I developed for my previous article, we can compare the efficiency of cipher suites providing forward secrecy:
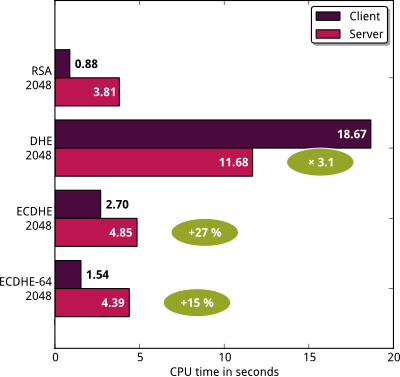
I have used a snapshot of OpenSSL 1.0.1 (2011/11/25). The
optimized version of ECDHE is the one you get by using
enable-ec_nistp_64_gcc_128 option when configuring OpenSSL.
Let’s focus on the server part. Enabling DHE-RSA-AES128-SHA cipher
suite hinders the performance of TLS handshakes by a factor of
3. Using ECDHE-RSA-AES128-SHA instead only adds an overhead of
27%. However, if we use the 64-bit optimized version, the cost is
only 15%. The overhead is only per full TLS handshake. If 3 out of 4
of your handshakes are resumed, you need to adjust the numbers.
Your mileage may vary but the computational cost for enabling perfect forward secrecy with an ECDHE cipher suite seems a small sacrifice for better security.
-
Perfect forward secrecy is an enhanced version of forward secrecy. It assumes each exchanged key are independent and therefore a compromised key cannot be used to compromise another one. ↩︎
-
For example, this is the case of the implementation I have proposed for stud to enable sharing of tickets between multiple hosts. ↩︎